Learning Objectives

Problem 1 of 3

A ferris wheel at an amusement park has riders get on at the bottom of the wheel which is 3 meters above the ground. The highest point of the ride is 21 meters above the ground and it takes 48 seconds to make a one complete revolution.

(a) Write two equations, one sine and one cosine, that models the height of a rider over time beginning from when they first start the ride.

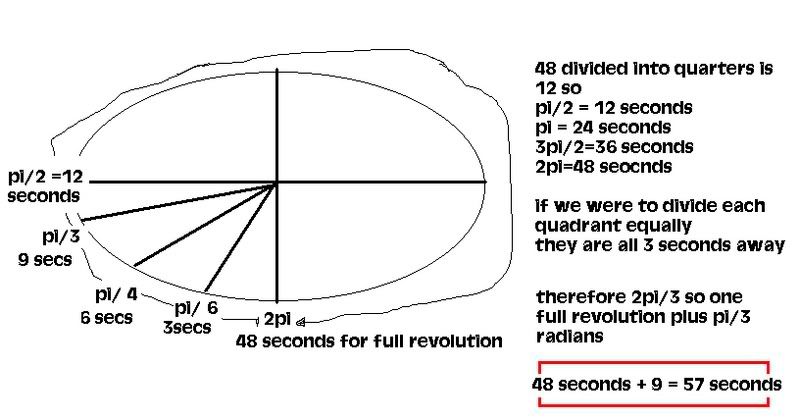
(b) How long would it take a rider to pass through an angle of 2π/3 radians?

(c) How long during each revolution is a rider higher than 10 meters above the ground?

Solution

a) H(t)= 3sin[(2π/48(t+0)]+12 and H(t)= -3cos[(2π/48)(t-12)]+12

b) it would take about 9 + 48 = 57 seconds to pass through the angle of 2π/3 radians

c) 10 = 3sin[(2π/48(t)]+12

let [2π/48(t)]=x

10=3sinx+12

-2=3sinx

sinx=-2/3

(48/2π)[2π/48(t)]= -2/3(48/2π)

t=-2/3(48/2π)

^^ i think..need my notes and calculator

still working on this...don't take..hehe sorry got no calculator on me right now..ill be back tomorrow =D

Problem 2 of 3

Determine the general solution algebraically. (Solve over the set of real numbers and write your answer accurate to at least 3 decimal places.)

Solution

Problem 3 of 3

A sinusoidal curve has a minimum point at (-π/3, -5) and the closest maximum point to the right is (π/6, 3).

(a) Determine an equation of this curve.

(b) Sketch the graph.

Solution